|
La differenza tra il navigare per aria o il camminare sulla terra sta nel
fatto che l'aria si muove.
Come un viaggiatore che si sposta in un vagone del treno "di suo" si muove
solo rispetto a tutti gli oggetti dello scompartimento, che gli appaiono
relativamente fermi, ma in realtà, oltre al suo movimento rispetto al
vagone, si muove sui binari con tutto il treno, un aereo vola all'interno di
una massa d'aria che a sua volta si sposta rispetto al terreno alla velocità
del vento.
Se il nostro aereo vola puntando il muso (la "prua") in una certa direzione,
il suo movimento complessivo non sarà diretto nello stessa direzione, ma, si
comporrà con lo spostamento di tutta la massa d'aria (il vento). |
 |
 |
|
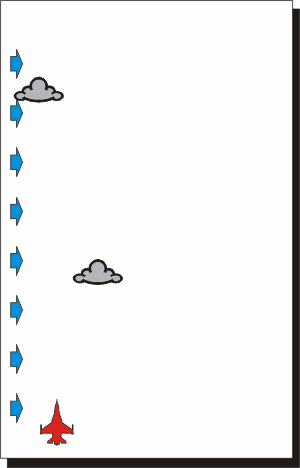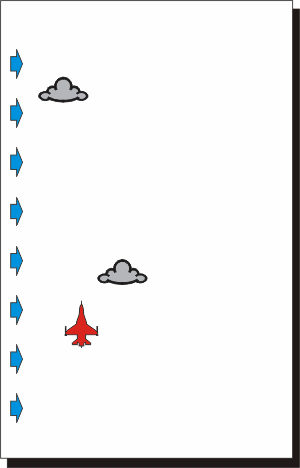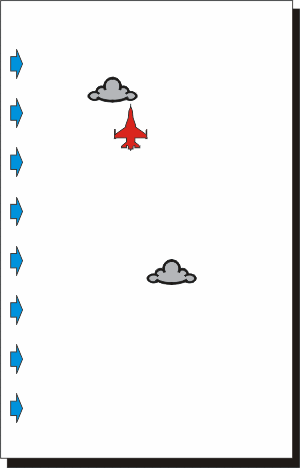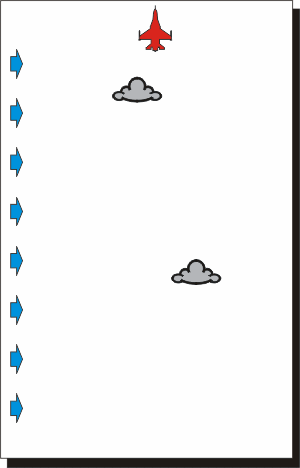
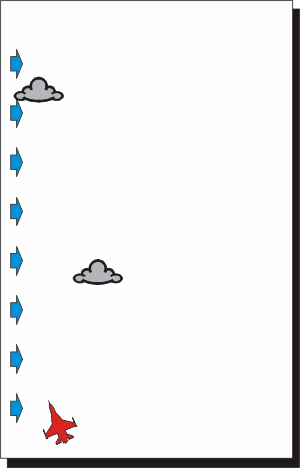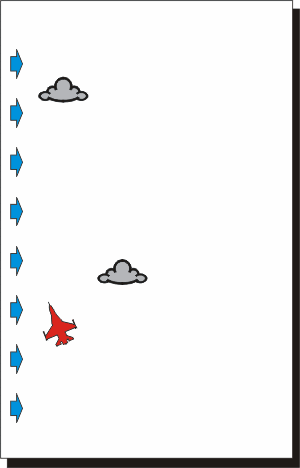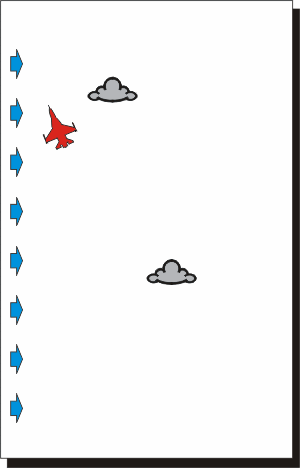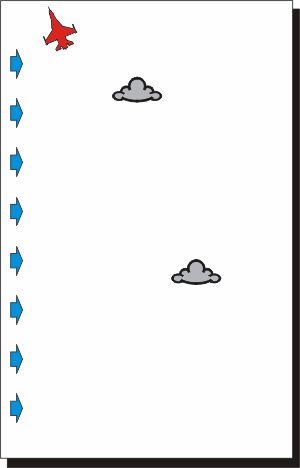
Nelle due rappresentazioni qui sopra si vede come un velivolo che si muove
in presenza di vento percorre la traiettoria indicata dalla sua prua, ma,
oltre ad avanzare, si muove insieme alle nuvole.
Se il pilota volesse mantenere la direzione prefissata dovrebbe inclinare la
prua di quel tanto che basta per contrastare il movimento dell'aria.
Il nostro problema sarà proprio sapere di quanto dobbiamo inclinare la prua,
in presenza di un dato vento, per mantenere la traiettoria che ci siamo
prefissati.
Intanto, giusto per parlare tutti la stessa lingua, definiamo alcune
componenti del nostro problema:
Chiamiamo TAS
(dall'inglese True Air Speed e cioè Velocità Vera
rispetto all'Aria) la nostra velocità rispetto alla massa d'aria, che
possiamo misurare con gli strumenti di bordo). |
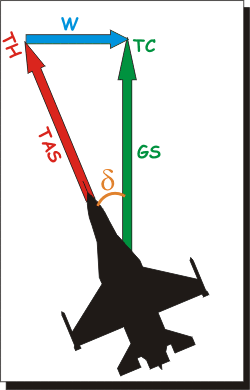 |
La velocità al suolo sarà la
GS (Ground Speed, e
cioè Velocità rispetto al Terreno).
Definiamo inoltre TH
(True Heading, Prua Vera) la direzione verso cui punta
il muso (che d'ora in poi chiameremo solo "prua") dell'aereo.
La TC (True
Course, Rotta Vera) sarà la direzione effettivamente
mantenuta rispetto al suolo (la "rotta").
L'angolo di deriva
δ
sarà la differenza tra la prua
TH e la
rotta TC.
Per rappresentare le velocità utilizziamo degli elementi grafici
presi in prestito dalla fisica: i "vettori".
Il vettore è semplicemente un segno grafico simile ad una freccia,
con cui si possono rappresentare la direzione (è la giacitura della
freccia), il verso (la punta della freccia) e il modulo (la
lunghezza della freccia) di una grandezza fisica quale sono velocità
e spostamento.
Per intenderci, se vogliamo rappresentare il moto di un aereo con i
vettori, disegneremo una "freccia" posizionata con lo stesso angolo,
rispetto ad una direzione di riferimento che nella realtà potrà
essere il Nord geografico, mentre sul foglio potrebbe essere
semplicemente la verticale, con cui si muove l'aereo, la punta della
freccia indicherà il verso con cui l'aereo si muove (da che parte
sta la prua) e la lunghezza della freccia sarà proporzionale al
valore della velocità espresso in nodi (kts - miglia marine all'ora)
o in Km/h. |
| L'unità di misura rispetto a cui dimensioneremo i
nostri vettori potrà essere scelta a piacere, importante sarà
mantenerla per la rappresentazione grafica di tutte le velocità
coinvolte nel problema. |
|
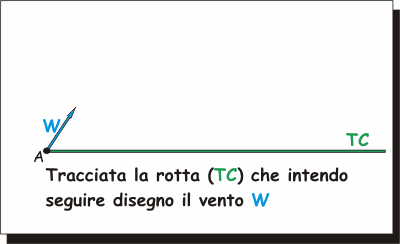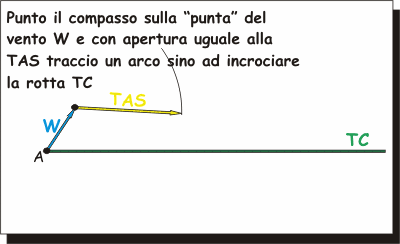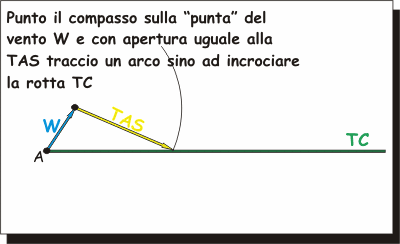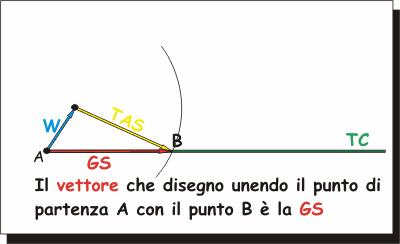
Con questo tipo di rappresentazione, risolvere il
problema di "che prua devo mantenere per essere sicuro, in presenza di
vento, di muovermi con una certa
TAS lungo una
rotta predefinita?" si riduce a disegnare un triangolo di cui siano note
le lunghezze di due lati (il vento e la
TAS) e l'angolo
compreso tra uno di questi e il terzo lato (cioè tra la direzione del
vento e la nostra rotta).
Come per tutti i problemi, se possiamo rappresentarli graficamente con
precisione, sarà il disegno stesso la soluzione.
Potrò cioè disegnare il triangolo e poi valutare l'angolo di prua
TH, la deriva e
la GS
semplicemente misurandoli proprio sul disegno stesso. |
 |
E' importantissimo capire con sicurezza il
significato delle linee tracciate.
Ripeto che la GS
è la somma tra vento W
e TAS, per cui
le due frecce W
e TAS si
"seguono" (la punta dell'una si appoggia alla coda dell'altra), mentre
la freccia GS
appoggia la punta alla più avanzata delle altre due e la coda alla coda
della più arretrata delle altre due.
Come per le normali somme aritmetiche, inoltre, non ha importanza se
metto prima il vento W
o la TAS (5+2
fa 7 tanto quanto 2+5).
E' lungo la GS/TC
che si muove il nostro aereo, la
TH rappresenta
solo la direzione verso cui punta la prua.
E' inoltre importante apprezzare che, per convenzione, del vento
W si indica la
direzione di provenienza (cioè a 180° rispetto alla direzione della
freccia che lo rappresenta - un vento da 040 "proviene" da 040 e si
muove verso 220). |
|