|
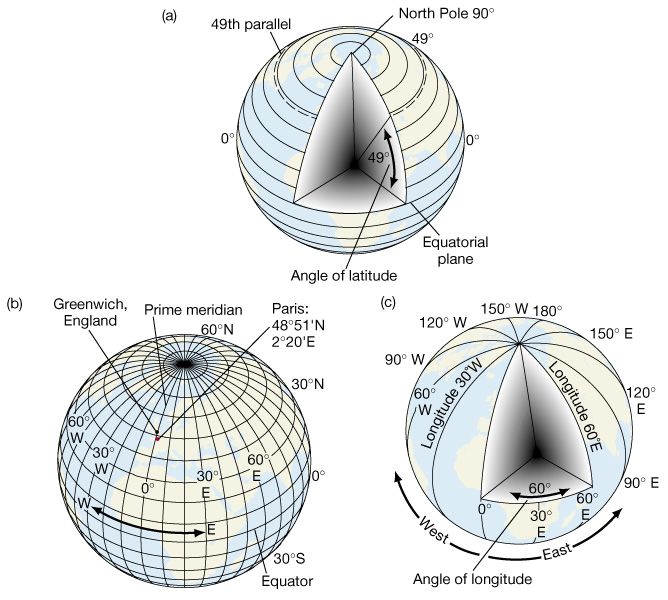
Per individuare un punto sulla superficie terrestre si utilizzano, come è
noto, due coordinate: la latitudine
φ e la
longitudine
λ.
Queste valori angolari che misurano rispettivamente l'angolo compreso tra il
piano equatoriale e la linea che unisce il punto P con il centro
della terra e l'angolo compreso tra il piano che contiene l'asse terrestre e
Greenwich (l'intersezione di tale piano con la superficie terrestre prende
nome di Meridiano Fondamentale) e il piano che contiene l'asse terrestre e
il punto P. |
|
|
 |
|
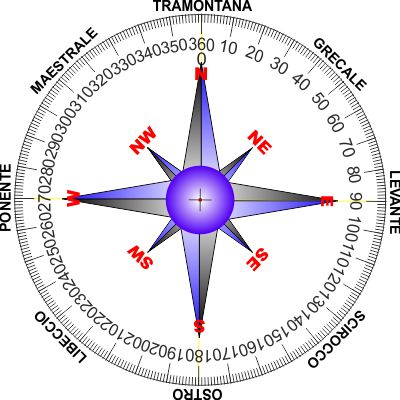
LA ROSA DEI VENTI |
Per convenzione le direzioni si misurano partendo dal Nord (è il "polo"
dal quale si vede la Terra girare in senso antiorario) in senso orario
per cui Est è a 90°, Sud a 180°, Ovest (West) a 270°.
I venti prendono nome e si riconoscono a seconda dalla direzione dalla
quale provengono.
- Nord - Tramontana
- Nord Ovest - Grecale
- Est - Levante
- Sud Est - Scirocco
- Sud - Ostro (o Mezzogiorno)
- Sud Ovest - Libeccio
- Ovest - Ponente
- Nord Ovest - Maestrale
|
|
Per rappresentare in modo "pratico" una piccola zona
della superficie terrestre, però, occorre "deformare" la sfera sino ad
appiattirla sulla carta geografica.
Che questa sia poi una proiezione di Mercatore o di Lambert, quando
l'area rappresentata è sufficientemente piccola per cui i meridiani
possano considerarsi tra loro paralleli (cosa che è vera per le carte di
Mercatore e approssimativamente vera per le carte di Lambert quando il
tratto considerato sia abbastanza breve), possiamo adottare un algoritmo
semplice ed efficace per passare dalle distanze misurate in Miglia
Marine (Nautical Miles) e angoli misurati in gradi e le coordinate
geografiche. |
|
Come prima cosa vediamo che relazione c'è tra il Miglio Marino e la
superficie terrestre.
Per convenzione il Miglio Marino equivale ad un primo di grado misurato su
un arco di cerchio massimo (e tutti i meridiani lo sono).
Pertanto si vede immediatamente come su una rappresentazione di qualsiasi
genere, andare in direzione Sud-Nord di un grado vuol dire percorrere 60
Miglia.
E questo sempre, qualsiasi sia la zona che andiamo a considerare.
Per la longitudine, invece, le cosa cambiano significativamente.
All'equatore, dove la longitudine varia lungo un cerchio anch'esso
"massimo", il Miglio Marino continua a corrispondere ad un primo di grado
anche di longitudine.
Al polo, invece, ad un giro completo di 360° di longitudine corrisponde una
lunghezza esattamente nulla.
Alle latitudini intermedie, ovviamente, avviene che un primo di longitudine
è genericamente "più corto" di un Miglio Marino. |
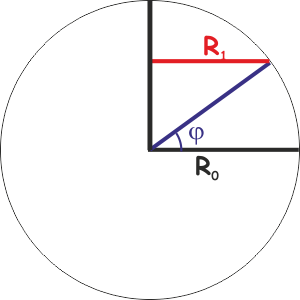
Facciamo una semplicissima considerazione:
All'equatore un Miglio Marino è uguale ad un primo di grado di
longitudine e cioè alla 21600a (360x60=21600)
parte della circonferenza terrestre, che a sua volta è uguale al
raggio terrestre R0 per 2π.
Ad una qualsiasi latitudine
φ, il
primo di grado di longitudine è uguale ancora alla 21600a
parte della circonferenza che stavolta non però più un cerchio
massimo, ma un cerchio generato da un raggio R1
individuato sul cerchio formato dall'intersezione tra il piano
parallelo all'equatore che passa per la latitudine
φ e la superficie terrestre.
Tra il raggio R1 e il raggio R0,
come si vede dalla figura, il rapporto è semplicemente cos
φ.
E', cioè, esplicitamente, R1=R0 cos
φ.
Da cui si ricava velocemente che alla latitudine
φ una differenza
Δλ
di primi di longitudine corrisponde ad una distanza in Miglia Marine
ΔNM =
Δλ cos
φ. |
 |
E, viceversa, una distanza in miglia marine
ΔNM
corrisponde ad una differenza di longitudine
Δλ =
ΔNM/cos
φ.
Consci di questo possiamo agevolmente passare dalle coordinate
geografiche alle distanze in miglia.
Vediamo un esempio: |
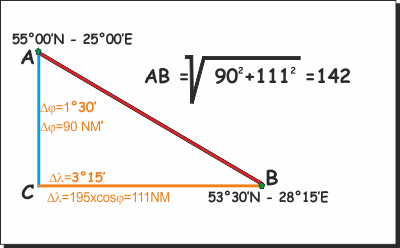 |
Dovevamo trovare la distanza tra i punti
A e B
conosciute le coordinate geografiche.
Abbiamo dapprima calcolato la differenza di latitudine
Δφ:
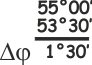
Come ben sappiamo 1° 30' corrispondono a
90' e come abbiamo appena visto, 90' di latitudine
corrispondono a 90 Miglia Marine. |
| Calcoliamoci quindi la differenza di longitudine
Dl:

Che sono 195' (3x60+15).
Dal momento che siamo alla latitudine di 55° (è abbastanza superfluo
chiedersi se utilizzare 55°, 53°30' o una media tra questi: il
coseno varia di valori impercettibili) 195' di
Δλ corrispondono ad una distanza
di 195 x cos 55° = 195 x 0.57=111 Miglia Marine. |
|
Per calcolarci infine la distanza tra
A e
B applichiamo il caro vecchio teorema di Pitagora al
triangolo ABC, rettangolo in
C.
Per trovare la rotta tra A e
B, dovremo calcolarci l'angolo
in A, che è:
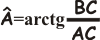
L'angolo di rotta sarà il supplementare dell'angolo in
A e cioè 180°-51° = 129°. |
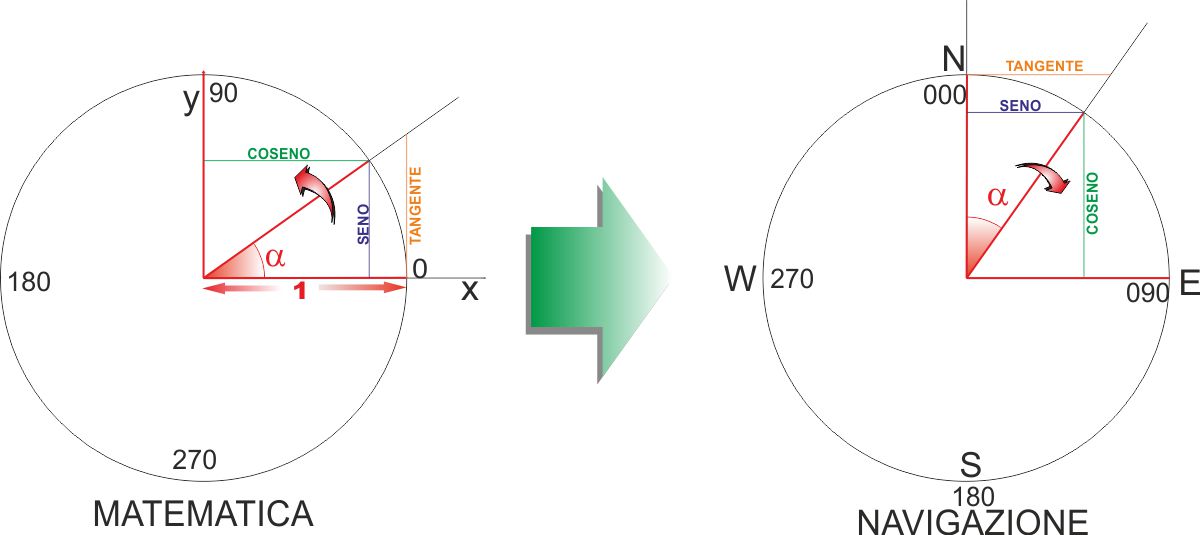 |
Nota : La trigonometria usata in navigazione è
(ovviamente) la stessa identica che si è vista nei corsi di matematica.
Cambiano però alcune convenzioni:
- Lo "zero" di riferimento in matematica è l'asse x orizzontale,
mentre per la navigazione lo "zero" è il Nord che convenzionalmente
è indicato in alto sull'asse verticale.
- Gli angoli "matematici" si misurano in senso antiorario, in
navigazione la "rosa dei venti" indica le direzioni in senso orario.
|
|