MATEMATICA
01 - SPICCIOLI DI TRIGONOMETRIA

1 2 3 4 5
6 7 8 9 10
11 12 13 14 15

LE FUNZIONI TRIGONOMETRICHE FONDAMENTALI
Vediamo nel modo più rapido e sintetico di cui sono capace che cosa sono le funzioni trigonometriche, e a cosa servono.
Intanto direi di partire da un principio fondamentale: quello della proporzionalità dei lati corrispondenti nei triangoli simili:
Se due triangoli sono simili (hanno gli angoli corrispondenti a due a due uguali)

Per essere ancora più semplici consideriamo solo triangoli rettangoli.
Ora costruiamo un cerchio di raggio unitario (uguale a uno, così le cose diventano ancora più semplici perché nella proporzione uno dei termini è UNO).
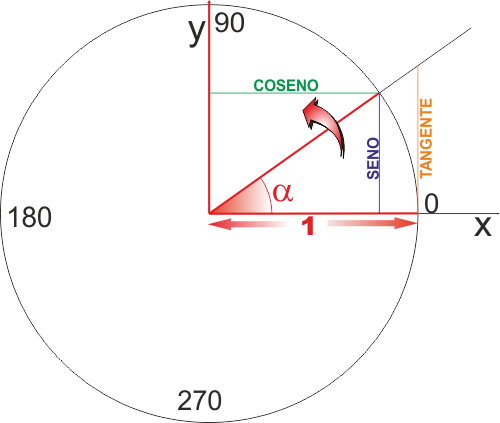
Sul primo quadrante di questo cerchio (da 0 a 90°) tracciamo un angolo qualsiasi α e dal punto in cui il lato di questo angolo incontra la circonferenza tracciamo le perpendicolari agli assi x e y.
Semplicemente, come indicato nella figura a lato, definiamo seno il lato parallelo all'asse y e coseno quello parallelo all'asse x.
Abbiamo costruito un triangolo rettangolo con l'ipotenusa che misura 1 (senza unità di misura UNO e basta).
Qualsiasi altro triangolo rettangolo che abbia un angolo uguale all'angolo α è simile a questo ed ha i lati in proporzione.
Ad esempio nel caso dei due triangoli a fianco sarà b1:1=a1:sen α che semplicissimamente vuol dire a1=b1 sen α
E nello stesso modo c1=b1 cos α.

Se invece di considerare l'ipotenusa b1 volessimo considerare il lato c1 come "riferimento", dovremmo utilizzare un'altra funzione detta "tangente" che è il segmento parallelo all'asse y, tangente alla circonferenza sull'asse x. In questo caso avremmo a1=c1 tg α .
In questo modo abbiamo un mezzo molto semplice per trovare i lati di un triangolo RETTANGOLO, una volta che ne conosciamo almeno uno e uno dei due angoli non retti.
Ancora più esplicitamente, visto che seno e coseno fanno riferimento all'ipotenusa di valore UNO, mentre la tangente fa riferimento al cateto di valore UNO, utilizzeremo:

  • Seno e coseno quando dobbiamo cercare un cateto e abbiamo l'ipotenusa (o in generale quando c'è di mezzo l'ipotenusa)
  • La tangente quando lavoriamo solo sui cateti

Mi fermo qui, per quello che serve per scomporre vettori e risolvere triangoli questo che abbiamo detto (e sono semplici DEFINIZIONI) e già sufficiente.

Da quello che abbiamo detto derivano due "proprietà" immediate di queste "funzioni trigonometriche".
La prima è che se applichiamo il teorema di Pitagora al nostro triangolo fatto da seno e coseno di un qualsiasi angolo e dall'ipotenusa che VALE 1 (e quindi 12 = 1) si ha:

1 = sen2α + cos2α

Cioè la somma dei quadrati di seno e coseno dello stesso angolo vale 1

Inoltre se osserviamo i due triangoli simili ... quello che ha come cateti seno e coseno e quello che ha come cateti la tangente e 1 (il raggio del cerchio) vediamo che:

tan α : sen α = 1 : cos α

che ci da un'altra proprietà semplice ma utile delle funzioni seno coseno e tangente:  tan α = sen α / cos α

 

SCOMPOSIZIONE DI VETTORI
Seni e coseni sono utilissimi quando, come spesso accade in fisica e in navigazione, ci troviamo a dover operare con dei VETTORI.
I vettori sono elementi utilizzati per rappresentare delle grandezze per le quali una semplice quantificazione "scalare" non sarebbe sufficiente.
Ad esempio ogni qualvolta ho a che fare con un movimento nello spazio o nel piano, non basta dire "mi sono spostato di 2 metri", perché per avere una descrizione completa devo dire anche "in che direzione" mi sono spostato di 2 metri.
Il vettore è quindi un segmento orientato (ha una punta ed una coda) di una certa lunghezza (la lunghezza del vettore si chiama MODULO).
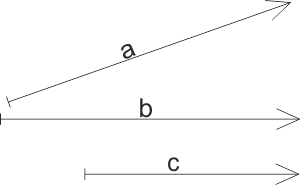Per chiarire, semplicemente, facendo riferimento alla figura a fianco, i vettori a e b hanno lo stesso modulo ma direzioni diverse, i vettori b e c hanno la stessa direzione ma moduli diversi.
Come con i numeri "scalari" anche con i vettori si possono fare somme e sottrazioni (anche moltiplicazioni e divisioni ma qui non ce ne occupiamo).
La somma di due vettori è semplicemente il vettore che risulta unendo la coda e la punta di due vettori posizionati consecutivamente (come nella figura qui sotto).
 

Nei due esempi sopra il vettore c è la somma dei vettori a e b.
Come potete immaginare fare i calcoli per risolvere "geometricamente" le due somme non sarebbe semplicissimo .. ma se invece dei vettori consideriamo le loro componenti ortogonali la cosa diventa molto più facile:
le due componenti ortogonali del vettore c sono "semplicemente" le somme delle componenti dei vettori a e b, che si trovano allineate e per le quali fare la somma è banale.
avremo, utilizzando seni e coseni come abbiamo visto prima:

  • ax= a cos α

  • bx= b cos β

  • ay= a sen α

  • by= b sen β

e quindi

  • cx = ax + bx

  • cy = ay + by

Con il teorema di Pitagora, se serve, possiamo poi trovare il modulo di c ... ma spesso anche di c ci conviene mantenere per successivi calcoli le componenti ortogonali cx e cy.

 

1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20