Cominciamo a parlare di "figure". Le figure si ottengono
componendo gli elementi primitivi che abbiamo visto nel capitolo
precedente.
Il componente più semplice che possiamo utilizzare è ovviamente la
retta (con i punti figure non ne possiamo generare perché sono
"adimensionali").
L'elemento che utilizziamo della retta sarà il SEGMENTO, cioè
una parte limitata della retta.
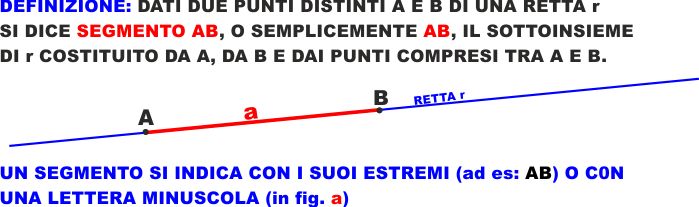
Siccome stiamo imparando ad essere rigorosi diamo una definizione
precisa ed utilizzabile di segmento (figura a lato).Ogni segmento
è quindi, come la retta, un insieme infinito e ordinato di punti, ma
se la retta è "illimitata", il segmento è "limitato".
I suoi limiti sono i punti estremi A e B, tutti i punti di r
compresi tra A e B sono INTERNI al segmento, tutti gli altri
sono ESTERNI.
I punti A e B sono gli ESTREMI del segmento AB.
|
 |
Essendo entità limitate, si possono confrontare tra
loro.
Se ho due segmenti posso spostarne uno (nella figura il segmento
g) in modo da far coincidere uno degli estremi con un estremo
dell'altro (nella figura il segmento a) e poi, vedi figura
qui sotto, possono capitare tre casi:
- Il secondo estremo cade all'interno dell'altro segmento, in
questo caso il segmento g è minore del segmento a
(g<a)
- Il secondo estremo coincide con il secondo estremo
dell'altro segmento, in questo caso il segmento g è
uguale al segmento a (g=a)
- Il secondo estremo cade all'esterno dell'altro segmento, in
questo caso il segmento g è maggiore del segmento a
(g>a)
|
|
 |
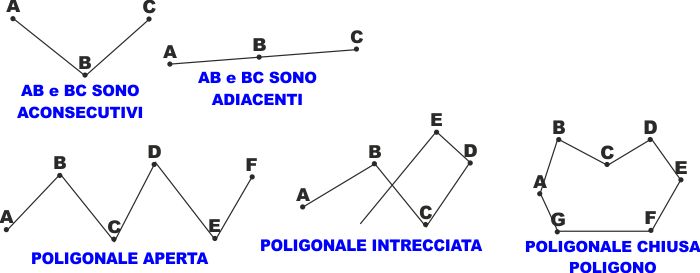
Due segmenti che abbiano in comune un estremo si dicono
CONSECUTIVI.
Se oltre ad avere in comune un estremo giacciono sulla stessa retta
sono anche ADIACENTI.Ne consegue che NON tutti i
segmenti CONSECUTIVI sono ADIACENTI, ma tutti i
segmenti ADIACENTI sono anche CONSECUTIVI
Si dice POLIGONALE l'unione di più segmenti a due a due
consecutivi ma non adiacenti.
- I segmenti che la compongono si dicono LATI mentre i
punti estremi dei segmenti che la compongono sono i VERTICI.
- Se il primo estremo del primo segmento coincide con il
secondo estremo dell'ultimo segmento la poligonale è chiusa ed è
un POLIGONO, se non coincidono la poligonale si dice
APERTA.
- Se due segmenti non consecutivi hanno un punto in comune la
poligonale è INTRECCIATA.
|
 |
|
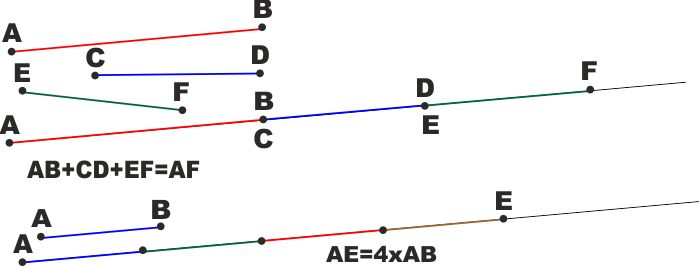 |
Spostando più segmenti in modo che risultino adiacenti, il
segmento ottenuto (che ha per estremi il primo estremo del primo
segmento e il secondo estremo dell'ultimo segmento) è la SOMMA
dei segmenti. Se sommiamo n volte lo stesso segmento (o segmenti
uguali) abbiamo il PRODOTTO di n segmenti.
In figura vediamo AF si dice multiplo secondo n (nella
figura n è 4) di AB
Nello stesso modo, facendo riferimento alla figura a lato, il
segmento AD è la DIFFERENZA tra il segmento AF
e il segmento DF. |
|
PIANI E SEMIPIANI |
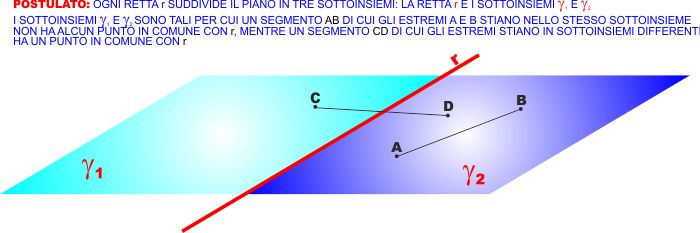
Vele il seguente POSTULATO:
Ogni retta r suddivide il piano in tre sottoinsiemi, la
stessa retta r e due sottoinsiemi
γ1 e
γ2 tali
per cui un segmento AB che ha gli estremi ambedue
nello stesso sottoinsieme
γ1
o
γ2
NON ha alcun punto in comune con r, mentre il
segmento CD i cui estremi appartengano a sottoinsiemi
diversi ha UN punto in comune con la ratta r
(interseca la retta r).
|
 |
DEFINIZIONE: si dice SEMIPIANO di origine
r ciascuno dei due insiemi di punti
γ1
U r e
γ2
U r (con
γ1 e
γ2
appartenenti allo stesso piano).
Due semipiani distinti di comune origine si dicono
OPPOSTI.Ne consegue che la retta r appartiene
ad ambedue i semipiani che genera.
E' cioè
γ1
W
γ2 = r
e che
γ1
U
γ2 = γ
(se
γ era il
piano da cui siamo partiti) |
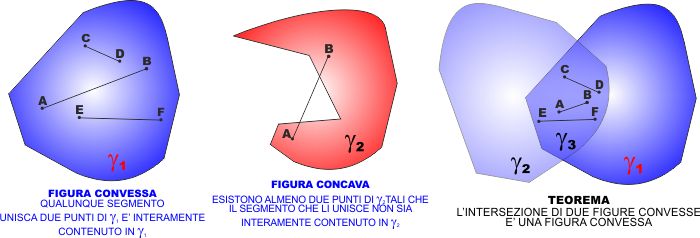
Figure CONCAVE e CONVESSE
Si dice CONVESSA una figura tale per cui comunque si
prendano due punti interni alla figura, tutti i punti che
compongono il segmento che li unisce sono punti appartenenti
alla figura.
Si dice CONCAVA una figura per la quale esistono
ALMENO due punti tali per cui il segmento che li unisce
non sia interamente formato da punti appartenenti alla
figura.
TEOREMA : L'intersezione di due figure convesse è una
figura convessa.
IPOTESI: Siano
γ1
e
γ2
due figure convesse, e sia
γ3
l'intersezione tra le due (
γ3 =
γ1
W
γ2 )
TESI : Vogliamo dimostrare che
γ3
è una figura convessa. |
 |
Come vedete la "dimostrazione" di un
TEOREMA si esegue partendo da un'IPOTESI, che
descrive la situazione di partenza .. quello che ho e che
so, e una TESI, che enuncia quello che voglio
dimostrare.
Il ragionamento che farò, partendo dalla ipotesi per
dimostrare la tesi potrà avvalersi SOLO di
affermazioni già riconosciute come vere, e cioè altri
teoremi già dimostrati, le definizioni che ho dato e i
postulati che ho accettato.
Nel nostro caso possiamo ragionare così:
Siano A e B due punti appartenenti a
γ3
. Dal momento che
γ3
è l'intersezione di
γ1
e γ2
(
γ3
=
γ1
W
γ2 )
tutti i punti di
γ3
appartengono anche a γ1
e a
γ2 e
quindi anche A e B.
Dato che
γ1
e
γ2
sono figure convesse, anche i rimanenti punti del segmento
AB appartengono sia a
γ1
che a
γ2
e di conseguenza appartengono a
γ3
che è la loro intersezione.
Quindi qualsiasi segmento AB io tracci unendo due
punti interni di
γ3
è composto solo da punti appartenenti a
γ3
che quindi, ricordando la definizione di figura
convessa, è una figura convessa. |
|
|
|
|
ANGOLI E STRISCE |
Vediamo cosa otteniamo quando intersechiamo due
semipiani originati da due rette differenti, nei vari casi
che si possono presentare:
Le rette come abbiamo visto possono essere coincidenti, e in
questo caso o lo sono anche i semipiani (stanno dalla stessa
parte) oppure questo sono opposti.
Le rette possono avere un punto in comune (si intersecano) e
in questo caso i due semipiani si intersecano anche loro,
oppure essere parallele (non hanno punti in comune). |
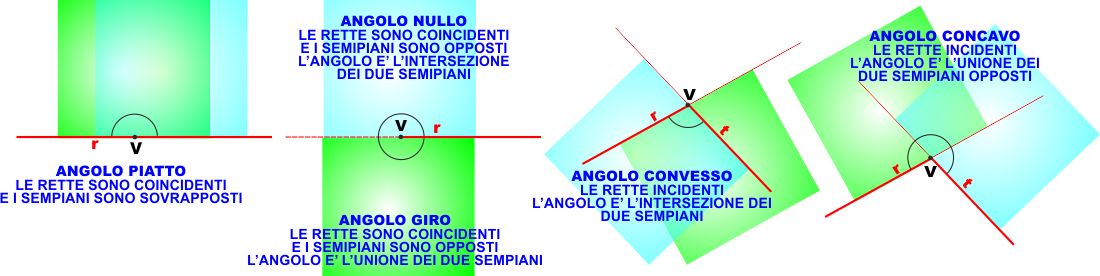 |
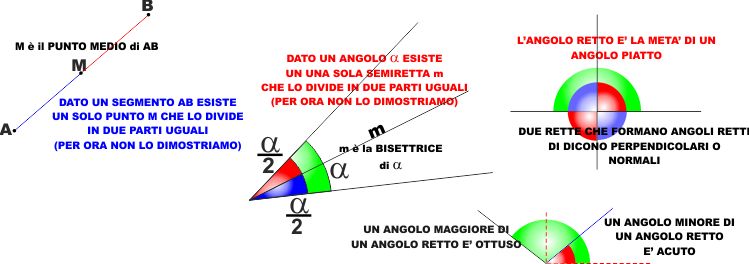
- Se le rette si intersecano in un punto V la
figura generata dall'intersezione dei due semipiani è un
ANGOLO e, per come abbiamo visto poco fa (ma
lascio a chi mi legge il compito di dimostrarlo), è una
figura CONVESSA - L'angolo è quindi un angolo
CONVESSO.
- Se le rette sono coincidenti si può prendere a
piacere un punto qualsiasi sulla retta (coincidono,
quindi la retta è una sola) e l'angolo è generato dalla
intersezione (in questo caso sovrapposizione) dei due
semipiani è detto ANGOLO PIATTO - anche qui si
può dimostrare che l'angolo piatto è una figura
convessa.
- Se invece i semipiani che si considerano sono
opposti, allora è possibile prendere un punto V come
origine di due semirette coincidenti e considerare o
l'intersezione tra i due semipiani (che è la sola
semiretta), e in questo caso avremo un ANGOLO NULLO,
o l'unione dei due semipiani e allora l'angolo sarà un
ANGOLO GIRO.
Potete vedere in realtà il caso di angolo nullo e angolo
piatto come i due casi limiti dell'angolo convesso
(diminuendone l'apertura sino a zero o aumentandola sino a
180°) e così l'angolo piatto e l'angolo giro come i casi
limiti per l'angolo concavo.
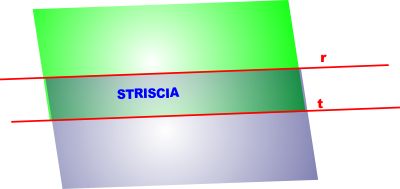
Se le due rette sono parallele (e quindi non hanno punti
in comune) l'intersezione tra i due semipiani da queste
generati è una STRISCIA. |
 |
|
|
Come per i segmenti anche per gli angoli esiste la possibilità di
confrontarli, e anche in questo caso due angoli possono essere uno
maggiore o minore dell'altro o uguali.
Come per i segmenti è possibile eseguire la somma di due angoli,
facendone coincidere un vertice e un lato (cioè rendendoli
consecutivi) e il prodotto secondo un numero n qualsiasi (sommando n
volte angoli uguali).
Si può quindi vedere un qualsiasi angolo come il prodotto di n
angoli uguali di misura unificata (unità di misura) e di conseguenza
è possibile "misurare" gli angoli.
Le diverse modalità di misura degli angoli le abbiamo già incontrate
nel capitolo precedente.
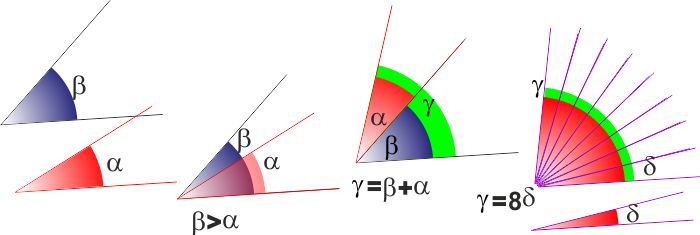
TEOREMA:
Somma e differenza di angoli uguali sono uguali.
IPOTESI :
α =
γ,
β
=
δ
TESI :
α +
β
=
γ +
δ |
 |
|
Dal momento che esiste un movimento rigido che mi permette di far
coincidere a con
g in quanto sono uguali, ed esiste un
movimento rigido capace di far coincidere b
e d, una volta che questi
coincidono, ponendoli consecutivi, quindi mettendo in comune il
vertice ed uno dei lati, anche tutti gli altri elementi della somma
saranno coincidenti.
Quindi gli angoli somma di angoli uguali sono uguali.
Nello stesso modo possiamo dimostrare il teorema per la differenza
tra angoli uguali e ancora per somma e differenza di segmenti
uguali. |
|
|
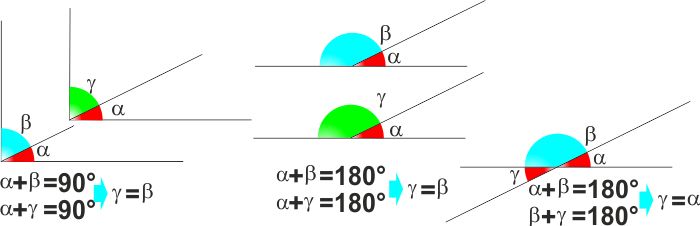 |
1° COROLLARIO - Angoli supplementari di angoli uguali sono
uguali 2° COROLLARIO - Angoli complementari di angoli
uguali sono uguali
3° COROLLARIO - Gli angoli opposti al vertice sono uguali |
|
|
TRIANGOLI |
|
Definizione di TRIANGOLO:
Il triangolo è un poligono
(linea poligonale chiusa vista nel capitolo precedente)
con tre lati e tre angoli.
Può essere descritto anche come intersezione dei tre angoli formati
a due a due dai lati o ancora come intersezione dei semipiani
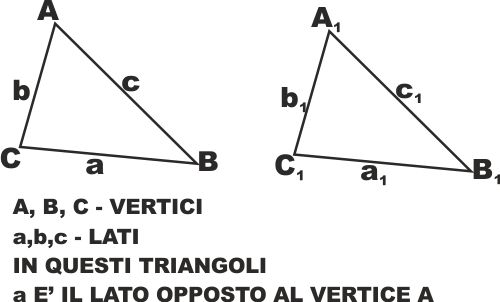
generati dalle rette che contengono i lati.Consideriamo due
triangoli uguali, cioè per i quali esiste un movimento rigido che li
porti a coincidere.
In questo caso il vertice A (vedi figura a lato) andrebbe a
coincidere col vertice A1, il vertice B con B1
e il vertice C con C1.
Quindi anche gli angoli in A, in B e in C sarebbero uguali agli
angoli in A1, B1 e C1.
Allo stesso modo il lato opposto ad A, che qui abbiamo chiamato a (o
BC) sarebbe uguale al lato a1, opposto al vertice
corrispondente A1.
Queste osservazioni, che possono sembrare banali, invece
risulteranno molto utili nei capitoli successivi.
In particolare l'ultima, che suona più o meno così,
in triangoli uguali ad angoli uguali sono
opposti lati uguali. |
 |
|
|
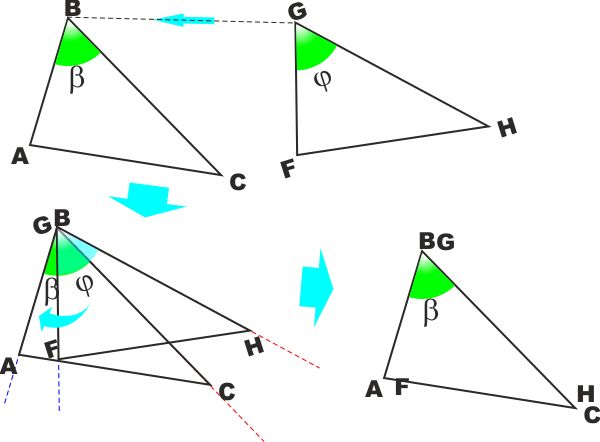 |
1° CRITERIO DI UGUAGLIANZA DEI TRIANGOLI:
Se due triangoli hanno due lati uguali e
l'angolo tra essi compreso uguale sono uguali.
IPOTESI: Di due triangoli ABC e FGH
è dato che AB = FG, BC = GH e
β (angolo in B) =
φ (angolo in G)
TESI : I due triangoli sono uguali, ovvero
esiste un movimento rigido che li porta a coincidere.
Siccome i due angoli
β
e φ sono uguali, esiste
un movimento che portando il vertice B a coincidere col
vertice G e ruotando opportunamente porta anche la semiretta
che contiene il lato AB a sovrapporsi alla semiretta che
contiene il lato FG e la semiretta che contiene BC a
sovrapporsi a quella che contiene GH.
Lo stesso movimento, oltre a far coincidere le due semirette fa
coincidere, visto che sono uguali, anche i due lati che sono
segmenti delle semirette.
E quindi anche il vertice A andrò a coincidere con il
corrispondente vertice F e il vertice C con H.
I due triangoli sono quindi sovrapponibili e quindi sono uguali.
|
|
|
|
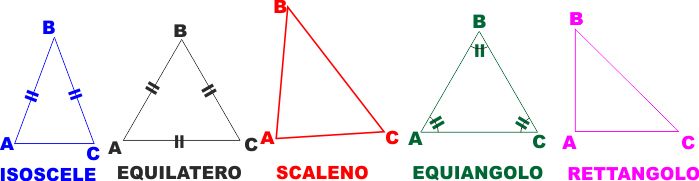
DEFINIZIONI: Un triangolo si dice:
-
ISOSCELE se ha due LATI uguali
-
EQUILATERO se ha tutti e tre i lati uguali
-
SCALENO se i suoi lati sono a due a due diversi
-
EQUIANGOLO se ha tutti e tre gli angoli uguali
-
RETTANGOLO se ha una angolo retto
|
 |
|
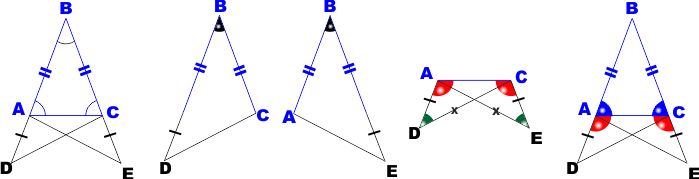 |
TEOREMA -
In un triangolo isoscele gli angoli alla base sono uguali
IPOTESI - E' dato un triangolo ABC di cui sappiamo
che i lati AB e BC sono uguali
TESI - Dobbiamo dimostrare che i due angoli alla base
A e C sono uguali |
|
|
Riportiamo sui prolungamenti dei lati AB e BC,
dalla parte dei vertici A e C due segmenti uguali AD e
CE, di lunghezza a piacere.
Congiungiamo D con C e A con E. Si ottengono i
triangoli DBA e ABE. Questi sono uguali in quanto:
Sono pertanto uguali per il !° criterio di uguaglianza dei
triangoli, hanno due lati e l'angolo tra essi compreso uguali.
Siccome in triangoli uguali a lati uguali stanno opposti angoli uguali, ne
ricaviamo che l'angolo in D è uguale all'angolo in E.
E siccome in triangoli uguali ad angoli uguali stanno opposti lati uguali,
anche AE = DC.
Andiamo ora a considerare i due triangoli DAC e
ACE.
Anch'essi sono uguali in quanto hanno:
-
AD = CE per costruzione (cioè perché li
abbiamo disegnati noi così)
-
l'angolo in D = angolo in E perché lo
abbiamo appena dimostrato
-
DC = AE perchè lo abbiamo appena
dimostrato
Allora anche gli angoli in A e in C di questi
triangoli (angoli DAC e ACE)
sono uguali.
Allora anche gli angoli alla base del nostro triangolo isoscele (BAC
e ACB) sono uguali perché supplementari
di angoli uguali.
COROLLARIO : Un triangolo equilatero è anche
equiangolo.
Non lo dimostro ma lo lascio fare a voi per esercizio. |
|
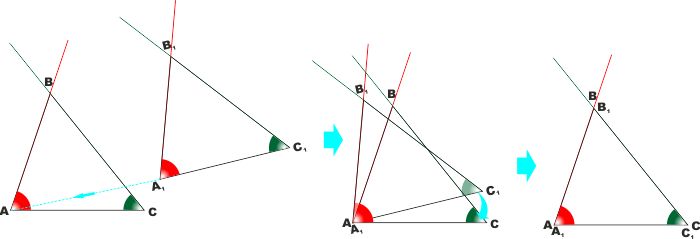 |
2° CRITERIO DI UGUAGLIANZA DEI TRIANGOLI:
Se due triangoli hanno due angoli uguali e il lato tra
essi compreso uguale sono uguali.
IPOTESI: Di due triangoli ABC e A1B1C1
è dato che AC= A1, C1 = c
e α (angolo in A) =
α1 (angolo in A1)
e γ (angolo in C) =
γ1 (angolo in C1)
TESI : I due triangoli sono uguali, ovvero esiste un
movimento rigido che li porta a coincidere.
Siccome i due lati AC e A1C1
sono uguali, esiste un movimento che portando il vertice A a
coincidere col vertice A1 e ruotando opportunamente porta
anche il vertice C1 a sovrapporsi al vertice C.
Lo stesso movimento, oltre a far coincidere i due segmenti fa coincidere,
visto che sono uguali anche gli angoli
α
e α1 e
γ e
γ1
e di conseguenza anche le due semirette che li
caratterizzano.
E quindi anche il vertice B andrò a coincidere con il corrispondente
vertice B1 in quanto punti in comune di due semirette
sovrapposte.
I due triangoli sono quindi sovrapponibili e quindi sono uguali
|
|
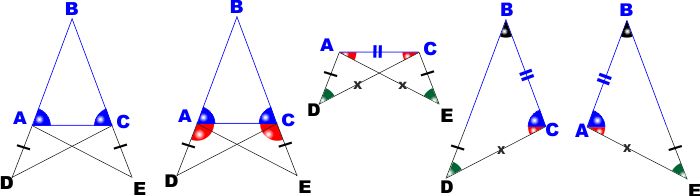
TEOREMA -
Se in un triangolo gli angoli alla base sono uguali, il triangolo è isoscele
IPOTESI - E' dato un triangolo ABC di cui sappiamo
che gli angoli alla base A e C sono uguali
TESI - Dobbiamo dimostrare il triangolo è isoscele
Il teorema è l'opposto del precedente, sono state quindi invertite ipotesi e
tesi.
Premetto che sarebbe il caso, prima di leggere la dimostrazione qui di
seguito, di provare ad eseguirla da soli.
Magari aiutandovi con la figura a lato, che dovrebbe già poter fornire buone
indicazioni ...
|
 |
|
Dimostrazione:
Come abbiamo fatto prima prolunghiamo i due lati AB e BC con i
segmenti uguali AD e CE.
Consideriamo i triangoli DAC e ACE, sono uguali in quanto :
Sono quindi uguali perché hanno due lati e l'angolo tra essi
compreso uguali.
Ne consegue che sono uguali gli angoli in D e in E opposti al
lato AC in comune e gli angoli in A (EAC)e in C
(DCA).
E sono anche uguali i lati DC e AE.
Quindi i triangoli DBC e ABE sono uguali perché hanno:
-
DC = AE perché lo abbiamo appena
dimostrato
-
Gli angoli in D e in E uguali perché
appena dimostrato
-
Gli angoli in C e in A uguali perché somma
dei due angoli alla base del triangolo ABC, uguali per ipotesi, e
dei due angoli EAC e DCE, uguali perché lo abbiamo appena
dimostrato.
Quindi se i triangoli DBC e ABE sono uguali lo
sono anche i lati AB e BC, opposti agli angoli uguali in D
e in E.
Come Volevasi Dimostrare (CVD). |
|
I due teoremi sui triangoli isoscele che abbiamo visto sono
l'uno l'opposto dell'altro.
Abbiamo cioè dimostrato che se un triangolo è isoscele ha gli angoli alla
base uguali e, viceversa, che se ha due angoli uguali è isoscele.
Solo ora possiamo quindi affermare che è CONDIZIONE NECESSARIA e
SUFFICIENTE (cioè occorre che sia così, ma se è così basta per
affermarlo) affinché un triangolo abbia due angoli uguali che esso sia
isoscele ed è ancora condizione necessaria e sufficiente perché un triangolo
sia isoscele è che abbia due angoli uguali.
COROLLARIO : Un triangolo equiangolo è anche equilatero.
|
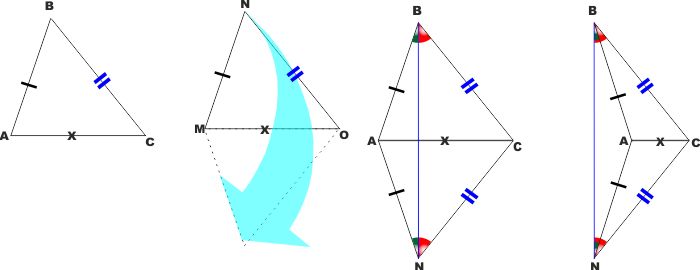 |
3° CRITERIO DI UGUAGLIANZA DEI TRIANGOLI:
Se due triangoli hanno tutti i lati a due a due uguali
sono uguali
IPOTESI: Di due triangoli ABC e MNO è
dato che AB= MN, BC= NO, AC= MO
TESI: I due triangoli sono uguali
"Ribaltiamo" il triangolo MNO e lo facciamo traslare
e ruotare in modo da far coincidere il lato MO con il lato AC
dell'altro triangolo e in modo che B ed N si trovino da parti
opposte e che i lati uguali BC e NO stiano dalla stessa parte
rispetto al segmento BN che tireremo a congiungere N con B.
Avremo così due triangoli ABC e ACN dei quali ACN è
palesemente uguale a MNO essendo lo stesso MNO traslato e
ribaltato.
Ci basterà quindi dimostrare che ABC sia uguale a ACN per
dimostrare la tesi.
Come ho già detto tracciamo il segmento BN e consideriamo i triangolo
NBC e NAB.
Essi sono isosceli in quanto sono uguali i lati NC = BC e
AN = AB.
Hanno quindi i due angoli in B ed in N uguali per i teoremi
che abbiamo appena dimostrato sui triangoli isosceli.
Gli angoli in N e in B dei triangoli ACN e ABC
sono quindi uguali perché somma di angoli uguali (può capitare che il
triangolo abbia un angolo ottuso - cioè maggiore di un angolo retto, in tal
caso saranno uguali in quanto differenza di angoli uguali, come si vede
nella figura più a destra).
I due triangoli sono quindi uguali perché hanno due lati e gli angoli tra
essi compresi uguali.
CVD
|
|
MEDIANE, ALTEZZE E
BISETTRICI DI UN TRIANGOLO |
|
TEOREMA: In ogni triangolo isoscele la bisettrice
dell'angolo al vertice è perpendicolare alla base e la divide in due parti
uguali.
IPOTESI . Un triangolo ABC è isoscele su base AC
TESI: La semiretta che biseca l'angolo al vertice B è
perpendicolare al lato AC e lo divide in due parti uguali.
Anche questa volta sarebbe opportuno che provaste da soli a
dimostrare questo teorema prima di proseguire a leggere la dimostrazione. |
 |
|
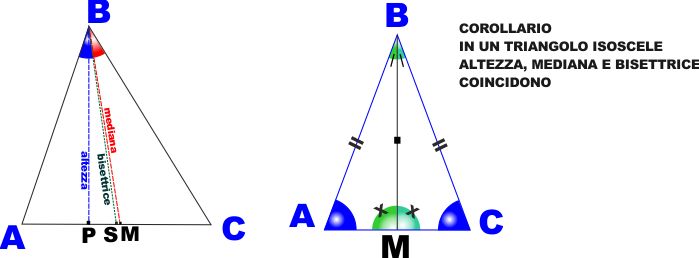 |
Dato il triangolo ABC, siano AB = BC.
Si tracci da B una semiretta che divida l'angolo B in due parti uguali. La
semiretta intersecherà il lato AC nel punto M, generando quindi due
triangoli ABM e MBC.
Questi due triangoli sono uguali, avendo l'angolo in B uguale per
costruzione (metà dello stesso angolo), il lato BM in comune e i lati AB e
BC uguali per ipotesi.
I due angoli con vertice M sono quindi uguali e di conseguenza dividono
l'angolo piatto in due parti uguali e sono quindi retti.
Per l'eguaglianza dei triangoli ABM e MBC anche i segmenti AM e MC sono
uguali e quindi dividono AC in due parti uguali.
CVD.
La semiretta tracciata da un vertice al lato opposto si
dice:
-
ALTEZZA, se è perpendicolare al lato
-
MEDIANA, se divide il lato in due parti uguali
-
BISETTRICE, se divide l'angolo in due parti
uguali
|
|
|






















